Using advanced models to unravel data values

As the world continues the drive toward greater digitalization, vast amounts of data are generated daily at a high frequency, bringing with it the challenge of dealing with high dimensionality data. High dimensionality data in statistics refers to data sets that contain many variables, potentially leading to increased computational time for modelling. In addition, such large data sets often produce a greater modeling challenge — sifting through potentially noisy and irrelevant information to extract the most important data. This can potentially affect the accuracy of our predictive models as well as making the results less interpretable. 

Without the proper use of advanced modeling techniques to understand the role of each variable, valuable insights are lost within the layers of dimension, letting redundant variables cloud the prediction capabilities of significant ones. High dimensionality data is just one of the many challenges that industry is required to combat; other issues such as poorly structured and managed data acquisition systems, inconsistency in data labeling and even the simple act of storing data sets with no intention of analyzing them are slowly turning data into the digital version of plastic. 

To prevent this, the use of machine learning models has become a popular tool to enable the extraction of hidden insights masked within the vast amount of data. Results have been shown to aid end users in decision-making processes and fault diagnosis, reducing the overall cost of operations. There are two main categories of machine learning models: supervised learning and unsupervised learning, each with its own advantages and disadvantages, and the decision on which one to choose is often based on the types of available data and the objectives of work. 

A supervised model requires the end users to know what physical conditions the data represents so the model can “learn” from the data and then make predictions, based on what it has learned, on another set of unseen data. Hence, the model is supervised and guided along the learning process and would therefore require labeled data. 

On the other hand, an unsupervised model does not need such information and is able to segregate the data into n number of groups based on how similar and different the data points are from each other. The model determines which group each data point belongs to without guidance from end users, but while the model has the ability to categorize, user intervention will still be required during post-processing to establish the nature of those categories. As a result, an unsupervised model is typically used for unlabeled data where we do not have information on the response variable. Consequently, a supervised model is often more accurate and reliable than the unsupervised approach due to the fact that we have information on the response variable and thus we can “teach” the model which types of data belong to what kind of condition before it needs to carry out a prediction. 

In an industry such as flow measurement, vast amounts of data are stored and generated by flowmeters, which have built-in digital transmitters outputting at a high frequency. This output contains valuable information on the performance of flowmeters as well as their operating conditions. However, storing data alone is not enough to unlock these opportunities. Data is only useful if appropriate modeling strategies are used to extract the underlying values and obtain new insights. 

Flowmeters such as ultrasonic meters (USMs) have the ability to produce a vast number of diagnostic variables indicating the condition and performance of meters under different operating conditions. To illustrate the capability and the advantages of using machine learning models as well as ways in which we can combat high dimensionality data, two case studies were conducted within TÜV SÜD National Engineering Laboratory, where machine learning models were used to analyze the historical data generated from USMs to predict the percentage of gas present within a single-phase fluid. The historical data was collected in experiments carried out on USMs with different manufacturers where various percentages of gas were deliberately injected into the water test line to examine the effect of gas concentration on the performance of USMs. Different gas volume fractions (GVF) ranging from 0.1% to 10% GVF were used. 

Case study 1: Detecting the presence of an unwanted second-phase using supervised models

The raw data from USM A contained 55 input variables with 13,055 observations and a standard data cleaning procedure was used to prepare the data prior to modeling. This includes removing missing values to ensure consistency in data labeling. The term “missing values” in statistics refer to no data value stored for a particular variable in an observation. The presence of missing values is common in practice. Therefore, care should be taken when dealing with missing values as they can have a significant impact on the conclusion made from your data. Some models cannot handle missing values; therefore, often it is compulsory to remove missing values prior to modeling. 

The “cleaned” data consisted of 55 variables with 12,286 observations, where only 11,081 observations were used to train and build the supervised machine learning model; the remaining data were used to further validate the prediction capability of the built model. This is a standard approach when building a supervised machine learning model to predict the classes of data, where the sample data is divided into two: (1) training data, where the model will learn the patterns and links between variables, and (2) validation data, where the model’s prediction ability will then be tested. Subsequently, new, unseen data is used to test the model’s generalization. In this case study, each class represents a different GVF.

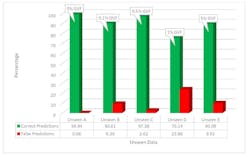
The supervised machine learning model achieved an accuracy of 98.62% in rightly classifying the data to the correct operating condition (i.e., the percentage of gas present within USM A). Further predictions were carried out on unseen data that was not used during the building stage of the model with the results shown in Figure 1.

The y-axis represents the percentage of predictions; the x-axis denotes the five sets of unseen data that were used to testify the model’s prediction capability. For unseen data A, the model predicted 99.94% of those data correctly to represent the condition where the fluid had 0% GVF, where it predicted falsely 0.06% of those to belong to other GVF groups. In other words, the model had predicted with a high accuracy that unseen data A was collected when the USM had no gas present within the fluid; therefore, it is highly probable that the flowmeter does not contain an unwanted second-phase based on the patterns observed by the model. 

On the other hand, for unseen data E, the model correctly predicted 90.09% of the data to be gathered when USM A was operated in an environment with 5% GVF present in the water (i.e., an indication of an unwanted second-phase present within the system), where 9.91% of data were falsely predicted to belong to other GVF groups. Similar interpretations can be made on the other unseen data groups. This type of prediction can help end users in decision-making processes relating to determining the severity of gas effects on meter output data. 

Furthermore, the model demonstrates the capability in successfully distinguishing different percentages of GVF, which could be used to monitor and alert end users of the presence of an unwanted second-phase, maintaining the quality and the reliability of output values. This would further improve the fault-diagnosis process by directing end users to data that contains the highest likelihood of being collected under a second-phase environment.

Case study 2: Overcoming the challenges arising from high dimensionality data 

The two-phase data used in Case Study 1 consisted of 55 variables with multiple, strong correlations with each other. This is known as high dimensionality data, which is becoming more and more common in a digitized world. It can be challenging for models to digest and sift out noisy information. For end users who do not necessarily possess the required knowledge in performing variable selection for different operating conditions, it is difficult to determine which variables are the most valuable; while some could be useful in other error detections, they could be misleading and redundant in identifying the presence of gas within the system. Consequently, a dimensionality reduction technique was used to reduce the number of dimensions needed to simplify the data analyzing process, while maximizing and retaining the most amount of valuable information.

A scree plot, shown in Figure 2, was obtained from the dimensionality reduction technique, which identifies the number of dimensions we should keep to retain the maximum amount of information from the original data. The amount of information retained from the original data is measured by the percentage of explained variances shown on the y-axis. The more variance a dimension can explain, the more information is retained from the original data. 

From Figure 2, we can see that by using the first two dimensions, they are able to explain around 59.4% of the variance that occurred in the original data. In other words, by reducing the original dimensions from 55 to only 9, the transformed data can already replicate 89.2% of variability shown in the original data. Although, we are ultimately losing some information by taking this approach, we have significantly reduced the number of dimensions while still retaining a high percentage of the useful information. The size of the percentage increase of explained variance decreases as we increase the number of dimensions. 

In other words, including an additional dimension will eventually add no significant values to the modeling results. Therefore, variables that contributed and correlated to the first and second dimensions are considered to be the most important and should be included. On the other hand, variables that are not correlated with the top dimensions or correlate with the last dimensions are variables with low contributions; therefore, they might be removed to simplify the data analyzing process.

Conclusion

In a digitized world, having too many variables is not necessarily advantageous and, in fact, can sometimes detrimentally affect the results of models as well as increase the computational time. Sometimes, certain variables can provide so much misleading information that they completely divert the model to a false conclusion. High dimensionality data also affect the interpretations of the model — the more layers/dimensions a data set contains, the harder it is to properly understand what is happening. 

The use of a dimensionality reduction technique is beneficial regardless of what types of machine learning models we are using. However, for an unsupervised learning model, removing irrelevant and confusing variables will significantly improve its prediction accuracy as well as its modeling speed, since it will have less trends, correlations and patterns to recognize. However, it is important to note that it is not easy to interpret the outputs resulting from dimensionality reduction techniques, as input variables have been transformed into a lower dimensionality space. 

In addition, results output from unsupervised learning models are less interpretable and less accurate due to no response variables, compared to a supervised learning model. Regardless of which modeling approach end users wish to take – supervised or unsupervised – the most crucial thing to remember is that data is only valuable if we explore and mine the values using modeling techniques.