Calculating the installed flow and gain of a control valve

When specifying a control valve, there are several tasks involved. First, the style of valve must be selected. This is often based on a combination of process parameters (such as pressure, temperature, corrosiveness of the media and abrasive properties), plant preference and economics. Next, the valve’s inherent flow characteristic (linear or equal percentage) needs to be selected. There are rules of thumb for selecting the inherent characteristic. For example, some authorities suggest a linear characteristic for systems that have very little dynamic pressure losses due to short pipe runs and few other pressure-consuming elements, such as isolation valves, elbows, heat exchangers, etc. For a system with long pipe runs and other pressure-consuming elements, an equal percentage valve is suggested.

The specifier must also have criteria in mind for how much of the valve’s control range should be used during normal operation. For example, it is often recommended that the valve be between about 60% to 80% open at the maximum required flow to provide sufficient, but not excessive, safety factor and, whenever possible, not much less than 20% open at the minimum required flow to avoid unpredictability of the flow characteristic below 10% opening. Once it is determined what valve style will be used, one of the many available valve sizing computer programs can be used to perform sizing calculations.

Two tools that can help the specifier in their selection of a valve are graphs of the installed flow characteristic¹ and installed gain² of all the valves that are being consideration for the application. Figure 1 shows the installed flow characteristic and installed gain for two possible valve selections (segment ball valves, which have an equal-percentage inherent flow characteristic) for the same application and where the process includes long pipe runs and a centrifugal pump. The 6-inch valve will control the full required flow range of 80 to 550 gpm over a travel range of 10% and a bit over 40% open, only 30% of its full travel capability, making flow quite sensitive to valve position changes. There is not much safety factor at the low end, and there is a lot of wasted flow capacity beyond the maximum flow of 550 gpm that is costly and unnecessary.

The 3-inch valve will control the full required flow range between about 22% open and about 72% open, 50% of its full travel capability, making flow less sensitive to valve position changes. The minimum and maximum specified flows are symmetrically placed on the valve’s installed flow characteristic, and there is about the same amount of safety factor at each end of the specified control range.

Typically, installed flow characteristics are graphed as relative flow versus relative travel as shown in Figure 1. That flow is graphed on a scale of 0 to 1, that is, from zero flow to 100% of the fully open flow, and valve travel is graphed on a scale of 0 to 1, that is, from fully closed to fully open. This graph gives a good visual representation of how linear the flow versus valve travel is and where the required flow range fits on the valve’s range of travel. What is missed with graphing relative flow is the relative slopes of the installed flow graphs of the valves being considered. If the two valves on the installed flow graph had been graphed with a vertical scale of gpm (or kg/h), the 6-inch valve’s graph would be much higher at 100% open (1.0% relative travel) and its slope would be much steeper.

Graphing the installed gain gives a different aspect to the installed behavior of a control valve and puts valves of different sizes and different styles on the same footing where they can be examined and compared. The gain of any device is defined as the rate of change of the output divided by the rate of change of the input. For a control valve, the input is the valve position, and the output is the flow through the valve. On the installed gain graph, the flow scale is shown as a relative flow with the reference point being the user’s specified maximum required flow rate. The user’s maximum specified flow rate is referred to as Qmax.

In Figure 1, 1.0 on the Q/Qmax scale represents the example’s maximum specified flow of 550 gpm, and 0.4 on the Q/Qmax scale represents 220 gpm. This is done so that that valves of different styles and sizes can be directly compared with each other.

Extremely low gains are undesirable because a low gain means when the valve moves, the flow does not change very much. It might not be so obvious why high gains are undesirable. An audio amplifier with a high gain may be desirable. But control valves are mechanical devices and, as such, parts that move while in contact with each other tend to stick when not moving. If a valve, because it tends to stick when not moving, can only be positioned within 2% of the desired position, and it has a gain of 4, the flow can only be adjusted within 8% steps, which may not be desirable. One valve manufacturer recommends the following gain criteria for installed gain within the specified flow range:

• Gain > 0.5
• Gain < 3.0
• As constant as possible
• As close to 1.0 as possible
• Gain (max) / Gain (min) < 2.0

The reason for limiting the change in gain within the required flow range to 2 to 1 is so that it will be easier to tune the controller for stable and fast response throughout the required flow range.

In addition to using the installed flow and gain analysis for comparing different valve sizes, it can be useful in comparing different valve styles in the same system. Suppose one has settled on a 10-inch segment ball valve for an application. The purchasing agent may point out that a 10-inch high performance butterfly valve would be much more economical. Segment ball valves typically have a close-to-perfect equal-percentage inherent flow characteristic, while high-performance butterfly valves have an inherent flow characteristic that is between linear and equal percentage. So, which one would be the best choice? It really depends on the system. A system with significant dynamic losses might be better controlled by the segment ball valve, but a system with intermediate dynamic losses might be better controlled by a high-performance butterfly valve. An installed flow and gain analysis could help in making the choice.

Some globe valves tend to have less-than-perfect inherent linear or equal-percentage inherent flow characteristics. Would an eccentric rotary plug valve be a good choice for a particular system?

A simple process model for creating installed flow and gain graphs is presented here. The method is based on the principle that piping pressure losses are approximately proportional to flow squared. This process model is only valid for fully turbulent flow and should be treated as an approximation.

To illustrate the method, it has been implemented here in Microsoft Excel. The author’s Excel worksheet is shown here divided into three tables. Tables 1 through 3 show sufficient detail so that anyone with experience with Excel should be able to implement a working Excel sheet. Alternately, the user could implement the method in their preferred programming environment. The method involves using one’s preferred control valve sizing software in conjunction with values of P1 and either P2 or Delta P calculated by the process model based on flow rates entered by the user in D25 of Table 1.

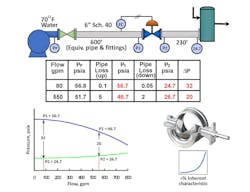
The sample calculations in Tables 1 through 3 are based on the system depicted in Figure 2. A static analysis of the system produced the pressure values shown in the table and shown graphically. The calculations are based on analyzing a 3-inch segment ball valve, which has an equal-percentage inherent flow characteristic. 

Because there is a significant amount of piping involved in the system, it turns out that the installed flow characteristic is close to linear.

The Δp used in the sizing calculation cannot be arbitrarily specified without regard for the actual system into which the valve will be installed. What must be kept in mind is that all of the components of the system except for the control valve (pipe, fittings, isolation valves, heat exchangers, etc.) are fixed, and at the flow rate required by the system (to cool a hot chemical to a specified temperature or maintain a specified level in a tank), the pressure loss in each of these fixed elements is also fixed.

Only the control valve is variable, and it is connected to an automatic control system. The control system will adjust the control valve to whatever position is necessary to establish the required flow and thus achieve the specified temperature, tank level or whatever. At this point, the portion of the overall system pressure differential (the difference between the pressure at the beginning of the system and at the end of the system) that is not being consumed by the fixed elements must appear across the control valve.

Making the calculations

In Table 1, based on the process model, flow entries in cell D25 will yield values of P1, P2 and delta P (the pressure drop across the control valve) at that flow. The only flow entry in D25 that requires any major effort on the user’s part is the flow when the valve being considered is fully open. This requires some simple guess work.

A good first guess would be to enter the specified required maximum flow increased by 10%. Using that first guess of flow, enter it into D25. Also, enter that flow guess along with P1 and either P2 or Delta P calculated in column D for that flow into your preferred control valve software and observe what percentage of valve travel the sizing program returns. The goal is to refine your flow guess (entered into the process model and the valve sizing program) until the valve travel is as close as possible to 100%.

Enter this fully open flow into the worksheet (shown in Table 2), cell L35, and then fill in row 35 with all the remaining flows. (Fully open flow X relative flow.) This could be done with simple formulas or manually. Also, complete column L with P1 and Delta P from the process model and CV and relative travel from your valve sizing program. The rest of the tabulated data can be filled in using the process model and your sizing program.

At this point, you have all the data needed to construct a graph of relative flow versus relative travel using the instructions in Table 2. Then, you have enough information to fill in the tabulated data for the installed gain graph table of Table 3 and construct the installed gain graph following the instructions in Table 3.

There are two ways you can mark the points of minimum and maximum specified flow on the installed flow graph. One way is that you can find where the relative minimum and maximum specified flows intersect the installed flow graph from your valve sizing calculation. The relative travel would have been calculated by your sizing program when you sized the valve for the minimum and maximum specified flow points as a percent opening. Divide this by 100 to get the relative travel. The second way is that you can find where the installed flow graph intersects the minimum specified flow on the relative flow scale at Qmin / fully open flow and where the installed flow graph intersects the maximum specified flow on the relative flow scale at Qmax / fully open flow.

On the installed gain graph, the given maximum specified flow is always at 1.0 on the Q/Qmax scale. The minimum design flow on the Q/Qmax scale is at Qmin/Qmax. These two points on the Q/Qmax scale of the installed gain graph will be the same for any valve sizes or styles that are being considered for the system represented by the user’s input of system parameters in column D, rows 9 to 14 of the process model, making it easy to compare their control capabilities. 

References

1. Monsen, Jon, An Insider’s Guide to Valve Sizing & Selection, Flow Control, February 2015, Vol. XXI, No. 2, pp. 29-32.
2. Monsen, Jon, An Insider’s Guide to Installed Gain as a Control Valve Sizing Criterion, Flow Control, May 2015, Vol. XXI, No. 5, pp. 22-25.